动态规划
矩阵连乘问题
1 |
|
数字三角形
1 |
|
红鲤鱼与绿鲤鱼
1 | 第15周任务-红鲤鱼和绿鲤鱼 |
- 如何推导出状态转移方程式动态规划的难点,例如本题的状态转移方程就是:
dp[1][i] = min(dp[0][i-1]), dp[1][i-1]) + (str[i] == ‘G’ ? 0 : 1);
即第i次染色的最少染色次数为:[0,i-1]区间最少染色次数加上当前是否染色。则完成了[0,i-1]到[0,i]区间最优解的转移。

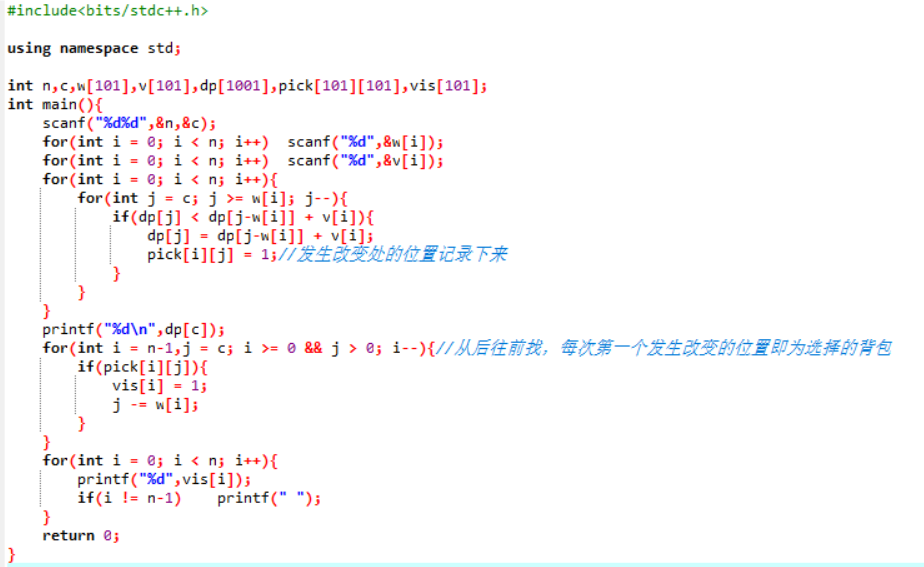
01背包
1 | 第15周任务-01背包 |
- 1、递归解法:
递归的方法较为直观,可以很直观的看出状态转移的思路。但是可能递归的中间过程比较难以想象。但是递归的思维方式比较简单,只需要抓住两点:递归终点和递归方程。终点就是在递归的边界情况的返回值,递归方程即从当前节点继续搜索子问题的最优解。注意结合这里递归方程理解dp中的状态转移方程。
- 很明显这种方式无法记录我们最后选择了那些物品,而且在递归的过程中存在很多不必要的搜索,所以我们需要用到记忆化搜索来剪枝并且记录节点的选择。

- 很明显这种方式无法记录我们最后选择了那些物品,而且在递归的过程中存在很多不必要的搜索,所以我们需要用到记忆化搜索来剪枝并且记录节点的选择。
- 2、递推解法
递推的方法其实也就是我们用到的双重循环,实际上我们可以把循环递推看成递归的一个逆过程。递归是当前不知道当前最优解,一直往子问题搜索,直到递归到子问题的边界然后开始回退,依次求出路径中的最优解。而递推则是通过已知的最优解通过状态转移方程逐步递推下一步的最优解,和贪心思想相似,只不过这里的最优解是动态的可修改的。我看见大家都是写的二维数组,这里我提供一个一维数组的方法。