S
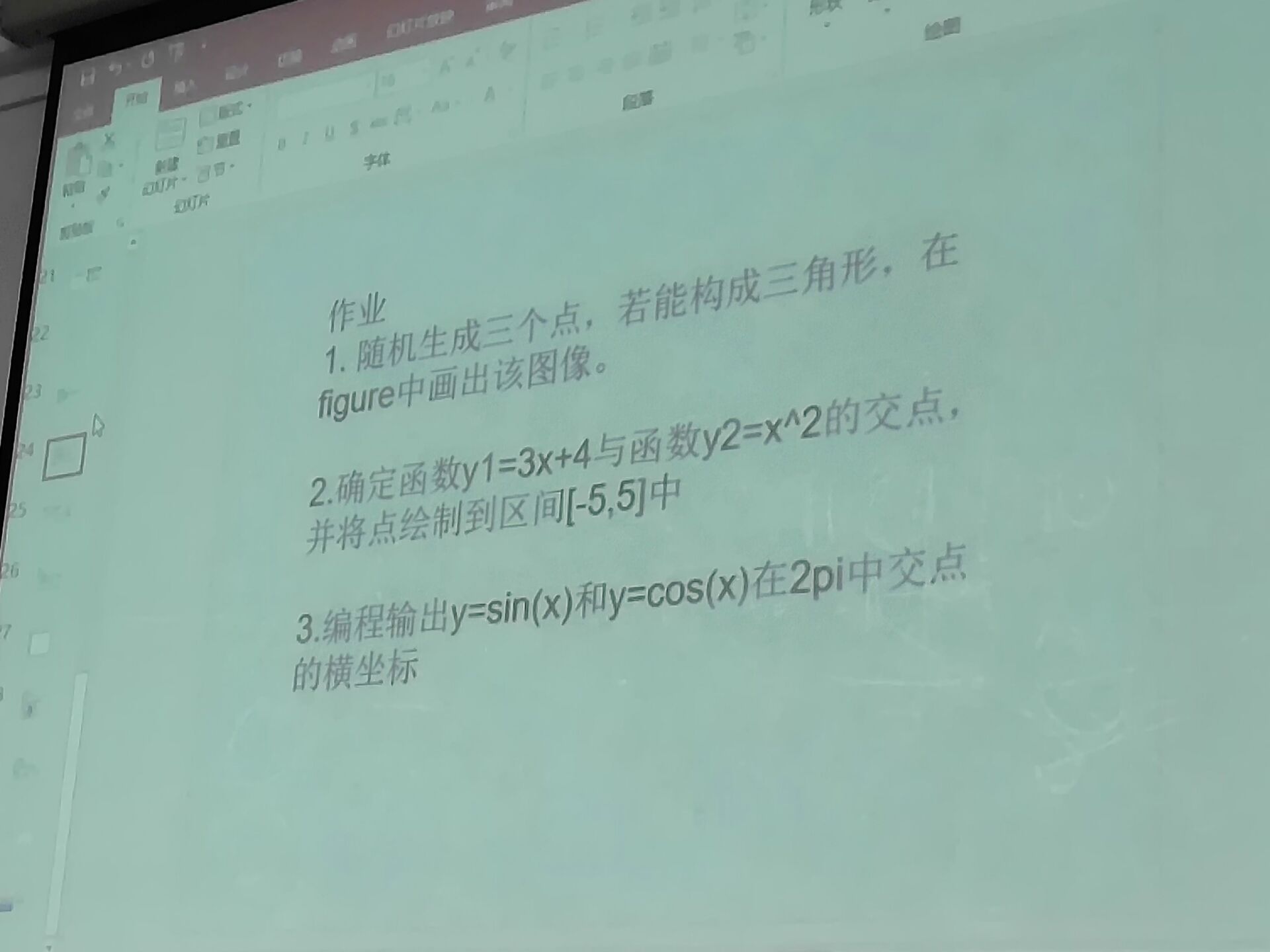

确定函数y1=3*x+4与函数y2=x^2的交点,并将点绘制到区间[-5,5]中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29%法一
clc,clear;
close all;
x = -5:0.01:5;
y1 = 3*x+4;
y2 = x.^2;
plot(x,y1,x,y2,'g')
hold on %如果不加这一句,画出的图像只有下面的交点
t=find(abs(y2-y1)<0.01);
a = [];
a(1) = 3*x(t(1))+4;
a(2) = 3*x(t(2))+4;
plot(x(t),a,'ro')
x(t) %输出后可知为行向量
%法二
clc,clear;
close all;
x = -5:0.01:5;
y1 = 3*x+4;
y2 = x.^2;
t=find(abs(y2-y1)<0.01); %t是包含两个下标索引的行向量
%交点横坐标是x(t(1))与x(t(2))
%x(t)就是包含2个横坐标的行向量
%plot画图注意维度一致
a = [];
a(1) = 3*x(t(1))+4;
a(2) = 3*x(t(2))+4;
plot(x(t),a,'ro',x,y1,x,y2,'g')两种方法图像是一样的
随机生成三个点,判断这三点是否能构成一个三角形若能构成三角形则输出其面积。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27%一
clc;clear;
a=rand(3,2);
d=squareform(pdist(a));
f=@(a,b,c)sqrt((a+b+c)/2*((a+b+c)/2-a)*((a+b+c)/2-b)*((a+b+c)/2-c));
s=f(d(1,2),d(1,3),d(2,3));
if s==0
fprintf('这三个点不构成一个三角形')
else
fprintf('这三个点构成三角形的面积为:s=%d\n',s)
end
%画出来/法二
clc,clear;
close all;
a = rand(3,2);
d = squareform(pdist(a));
if d(1,2)+d(1,3) > d(2,3)&d(2,3)+d(1,3) > d(1,2)&d(1,2)+d(2,3) > d(1,3)
e = d(1,2)+d(1,3)+d(2,3);
s = sqrt(e*(e-d(1,2))*(e-d(1,3))*(e-d(2,3)));
x = [a(:,1);a(1,1)];
y = [a(:,2);a(1,2)];
plot(x,y)
fprintf('三角形面积为:s=%f\n', s )
else
disp('无法构成三角形')
end输入绳子的长度n,将该绳子分成三段,每段的长度为正整数,输出由该三段绳子组成的三角形个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14%暴力法 不推荐
clc;clear;
n=input('the length of string is ');
num=0;
for i1=1:n-2 %三个边长的穷举
for i2=i1:n-1-i1
i3=n-i1-i2;
if i1+i2>i3 && i1+i3>i2 && i2+i3>i1 && i3>=i2
num=num+1;%计数加一
fprintf('the num is %d %d %d\n',i1,i2,i3);
end
end
end
fprintf('长度为 %d 的绳子分成三段可以组成 %d 个三角形\n',n,num);一个不透明的袋子中放了黑白各一球(除了颜色,其他均相同)。随机从中取出一球,如果取到黑球,则将此球放入袋中,摇匀,继续取,直到取出白球才结束。问:取到白球所需次数的数学期望
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30%方法一
clc;clear;
t=solve('1*( 1/2)+( 1+ t )*( 1/2)-t');%原理数学期望文章里有
t
%二
%函数
clc,clear;
syms k;
symsum(k*(1/2)^k,k,1,inf)
%三
clc,clear;
rand('state',sum(100*clock))
a = 0;
for i = 1:inf
j = randi(2); %生成[1, 2]的整数
if j == 2 && i > 20
%p避免偶然性,实验次数要多一点,所以i>20
%因为取出的白球1/2概率太大,实验次数无法达到那么多
%所以将20次前的取出的白球与黑球,都当作白球处理,后面正常处理
break;
end
a = a+1;
end
t = 0;
for k = 1:i
t = (1/2)^(k)*k+t;
end
t一只失明的小猫不幸掉进山洞里,山洞有三个门,一个门进去后走2h可以回到地面,从第二个门进去后走4h又回到原始出发点,不幸的是从第三个门进去后走6h还 是回到原始出发点。猫每次都是随机地选择其中一个门走。那么可怜的小猫走出山洞的时间期望是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24%法一
clc,clear;
s=0;
for i=1:10000
a=randi([1,3]);
while a~=1
if a==2
s=s+4;
else
s=s+6;
end
a=randi([1,3]);
end
s=s+2;
end
fprintf('小猫走出山洞的时间期望为%d\n',s/i);
%法二
%设未知数期望时间为t,小猫选择第二或第三个门的情况,走完4h,6h,后又回到了原点,
%接下来走出去所花费的时间就是期望时间了
%t =2×( 1/3)+( 4+ t )×( 1/3)+( 6+ t )×1/3 解方程得 t =12
clc;clear;
t=solve('2*( 1/3)+( 4+ t )*( 1/3)+( 6+ t )*1/3-t');
fprintf('小猫走出山洞的时间期望为%d\n',t);生成一个5*5的随机矩阵A,并计算A的两条对角线之和。
1
2
3clc,clear;
a = rand(5,5);
b = sum(diag(a)+diag(a')) - a(3,3)任意输入一串数字,输出这一串数字所组成的最大数字和最小数字。
1
2
3
4
5
6
7
8
9
10clc,clear;
a = input('a = ');
b = num2str(a);
c = length(b);
d = [];
for i = 1:c
d(i) = str2num(b(i));
end
sort(d)%该题没考虑首位为0情况,注意,出题人也没设置
sort(d, 'descend')求100以内素数的和
1
2
3clc;clear;
a=primes(100);
sum(a)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38%法一
clc; clear;
close all;
x=-3:0.01:4;
y=sqrt(1-(x).^2).*(x>=-1&x<0)+2.^(x).*(x>=0&x<2)+(x+1).*(x>=-3&x<-1)+4*(x>=2);
%注意括号!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!特别是对x的括号!多加可以防止错误发生
%按我的理解,因为x的范围构成了一个矩阵(很多个横坐标),所以对于图里面第二个函数与第三个函数,是点乘,因为要算出每一个横坐标的纵坐标,所以
%用点乘使得每个元素运算,如果去掉会报错
plot(x,y)
clc;clear;
close all;
x = -3:0.01:4;
y = 4*(x>= 2)+2.^x.*(x >= 0&x < 2)+sqrt(1-x.^2).*(x>=-1&x<0)+(x+1).*(x >= -3 & x < -1);
plot(x,y)
%法二,看看就行,算了,别看了,垃圾写法
clc,clear;
close all;
y1 = 4*ones(1,21);
x1 = 2:0.1:4;
plot(x1,y1)
hold on
%que
x2 = 0:0.01:2;
y2 = 2.^(x2);
plot(x2, y2)
hold on
x3 = -1:0.001:0;
y3 = sqrt(1-(x3).^2);
plot(x3,y3)
hold on
x4 = -3:0.001:-1;
y4 = x4+1;
plot(x4,y4)任意给出一个矩阵,找出矩阵中大于平均元素的元素,并存放于另一个矩阵中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20%法一
clc;clear;
a=rand(3);
s=[ ];
m=mean(a(:));
for i=1:9
if a(i)>m
s=[s;a(i)];
end
end
s
%法二
clc;clear;
a=rand(3);
b=a(:);
m=mean(b);
c=max(b,m);
c( find(c==m) )=[ ]; %这里有关于查找数组满足条件元素其它方法,在矩阵操作补充里
c任意给出一个矩阵,求删除周围元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23clc;clear;
m=input('m=');
n=input('n=');
a=rand(m,n)
a( [1 end] , : )=[ ];
a( : , [1 end] )=[ ];
a
%answer
a =
0.8147 0.0975 0.1576 0.1419 0.6557
0.9058 0.2785 0.9706 0.4218 0.0357
0.1270 0.5469 0.9572 0.9157 0.8491
0.9134 0.9575 0.4854 0.7922 0.9340
0.6324 0.9649 0.8003 0.9595 0.6787
a =
0.2785 0.9706 0.4218
0.5469 0.9572 0.9157
0.9575 0.4854 0.7922以最短的程序创建一个10*10的矩阵,要横着数的从1到100。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17clc;clear;
a=1:100;
b=reshape(a,10,10)
c=b'
%answer
c =
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100随机生成某数列,求四周元素的平均值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27%法一
clc;clear;
n=input('n=');
m=input('m=');
a=rand(m,n)
x=[ ];
for i=1:m
for j=1:n
if i==1 || i==m || j==1 || j==n
x=[x a(i,j)];
end
end
end
mean(x)
%法二
clc;clear;
n=input('n=');
m=input('m=');
a=rand(m,n)
x=[ ];
b = a( [1 end] , : );
x=[x;b(:)]; %注意这种方法
a( [1 end] , : ) = [];
c = a( : , [1 end ] );
x=[x;c(:)];
mean(x)