matlab矩阵以及常用函数

函数调用

• 调用函数文件的一般格式为 [输出参数表]=函数名(输入参数表)
• 调用函数时应注意： 当调用一个函数时，输入和输出参数的顺序应与函数定义时的一致，其数目可以 按少于函数文件中所规定的输入和输出参数调用函数，但不能使用多于函数文件所规定的 输入和输出参数数目。如果输入和输出参数数目多于或少于函数文件所允许的数目，则调 用时自动返回错误信息。
• 当函数有一个以上输出参数时，输出参数包含在方括号内。例如，[m,n]=size(x)。 注意：[m,n]在左边表示函数的两个输出参数 m 和 n；不要把它和[m,n]在等号右边的情况混 淆，如 y=[m,n]表示数组 y 由变量 m 和 n 所组成。

矩阵

• 下标从1开始
• 矩阵里面元素可以是符号与字符（‘a’,’,’）,输入的元素维度要一样
  • 矩阵里面的元素也可以是矩阵，但是矩阵长度维度必须与其它元素相同
• 生成10*10的矩阵可以如下：a = [1:10;11:20;21:....];就是运用：
• 对矩阵a第一行后面2个赋予其他值(灵活运用：)

a = [1 2 3
	4 7 8
	1 2 5];		 
a(1,2:3) = x;

• 对一个矩阵A赋值提取可以取出然后赋给一个小矩阵a

• 矩阵的下标也可以是向量。
  • 例如 b=a(x,y)；可以得到一个矩阵 b。a 的行标来自向量 x，而列标来自向量 y。 例如，矩阵 a 有 n 列，那末 b=a(:,n:-1:1) 将得到矩阵 b，它等于矩阵 a 按列的逆序排列。

• a(end:-1:end-5, 3)是最后一行到倒数第6行的所有第三个元素

• 删除矩阵某行某列a(i,j)=[];

• 如果要将一个矩阵存储在计算机中，MATLAB 规定矩阵元素在存储器中的存放次序是 按列的先后顺序存放，即存完第 1 列后，再存第 2 列，依次类推
  • 作为矩阵的特例，一维数组或者说向量元素是依其元素本身的先后次序进行存储的。
  • 必须指出，不是所有高级语言都这样规定矩阵(或数组)元素的存储次序，例如 C 语言 就是按行的先后顺序来存放数组元素，即存完第 1 行后，再存第 2 行，依次类推。记住这 一点对正确使用高级语言的接口技术是十分有益的。

• clc;
  clear;
  a=[2 5 6 9 8 86 4 5 6 65 3 54];
  m=a(1);
  for i=1:12
  	if a(i)>m
  		m=a(i);
  	end
  end
  		m
  	
  a=[1,2,3,4,5,6,7];
  for i=1:7
  	a(i)=a(i)+1;
  end
  
  clc,clear
  A=[0.5,1.732,0.618,3.1415,1.6,0.9];
  for i=1:6
       for j=i:6
            if a(j)<a(i)
  		      a(i)=a(i)+a(j);
  		     a(j)=a(i)-a(j);
  		     a(i)=a(i)-a(j);
  		 end
  	end
  end
  
  
  clc,clear
  for i=1:15
  	for j=1:15
  	     if i+j==15&&4*i+2*j==40
  		     fprintf(‘兔%d只,鸡%d只\n’,i,j);
  	     end
  	end
  end

矩阵除法

• 解线性方程组时，我们需要用到矩阵的除法。
  • a为系数矩阵，b为结果矩阵，x为解集矩阵。
  • 当遇到A*X=B时，两边左除A，X=A\B。
  • 当遇到X*A=B时，两边右除A，X=B/A。
• 如果我们需要矩阵A与B对应元素相除，依旧点除。

矩阵旋转

• 对于函数rot90顺时针旋转90度，可以rot90(a,3);或者rot90(a,-1);
• fliplr(A)左右旋转，就是最后2个字母l，r即left,right
• flipud(A)上下旋转，就是最后2个字母u,d即up,down
• B = fliplr(A) 返回 A，围绕垂直轴按左右方向翻转其各列。
  • 如果 A 是一个行向量，则 fliplr(A) 返回一个相同长度的向量，其元素的顺序颠倒。如果 A 是一个列向量，则 fliplr(A) 只返回 A。对于多维数组，fliplr 作用于由第一个和第二个维度构成的平面。
  • fliplr(A) 等效于 flip(A,2)。

reshape函数

• 按列优先

size函数

矩阵元素的操作

• 取矩阵A的第i1~i2行、第j1~j2列构成新矩阵:A(i1:i2, j1:j2)
• 以逆序提取矩阵A的第i1~i2行，构成新矩阵:A(i2:-1：i1，:）
• 以逆序提取矩阵A的第j1~j2列，构成新矩阵:A(:, j2:-1：j1）
• 删除A的第i1~i2行，构成新矩阵:A(i1:i2，：)=[ ]
• 删除A的第j1~j2列，构成新矩阵:A(：， j1:j2)=[ ]
• 将矩阵A和B拼接成新矩阵：[A B]；%行连接[A；B]%列连接

按照matlab中列优先提取

• 形如a(k)的都是单下标索引，按照列优先原则

• 想提取出a的2、5两个元素，并放入新矩阵中，可以使用a( [ 2 5 ] ),

  • 2和5必须用[ ]括起来,否则像a(2 5)计算机是读不出来的。

• 同理，提取a( [ 1 3 5 ] )是提取第1、3、5个矩阵并放入同一行，此时也可以使用a(1:2:5)，因为冒号存在，没有[ ]计算机也知道它的意思。

• 如果我要把第1、3个元素放入第一行，第2、4个元素放入第二行，可以a( [ 1 3;2 4 ] )。

• a( [1,2,3] )逗号,空格都用来分隔

• 栗子:

  clc,clear;
  close all;
  a = [1 2
      3 4
      5 6];
  a([1 2],[1 2]) %双下标索引
  a([1 2])
  a([1 3; 2 4])
  
  %answer
  %第一行与第二行和第一列与第二列相交的元素
  ans =
  
       1     2
       3     4
  
  
  ans =
  
       1     3
  
  
  ans =
  
       1     5
       3     2

• a(:)代表提取a矩阵所有的元素，原理是排序法则(列优先)。

  • a( : , : )也是提取a矩阵所有的元素，与原矩阵相同

双下标索引

• 若a是已知的矩阵，a( [ 1 3 ] , [ 2 4 ] )的意思是：把a第1、3行和第2、4行相交的元素，放入新矩阵中。并且位置和原来保持一致。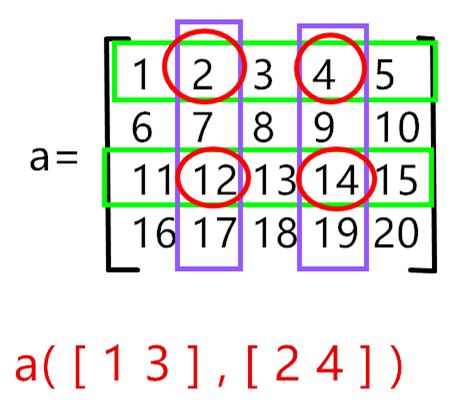
  
  

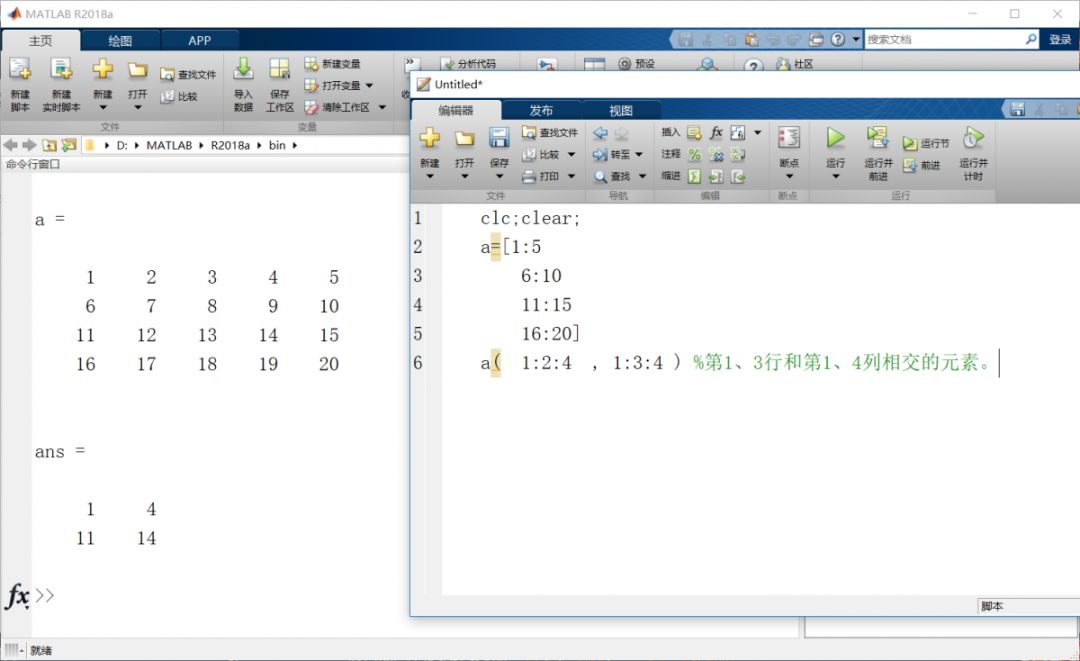
矩阵乘法

• matlab 中.和有什么区别简单的说:
  • *代表变量相乘，或者矩阵相乘
  • .* 是矩阵中对应位置变量相乘，组成新得矩阵
    • 例如

      [1 2 3].*[3 4 6]=[3 8 18]
      但是[1 2 3] * [3 4 6]就是语法错误！
      另外[1 2; 3 4] .*[5 6;7 8]=[5 12;21 28]
      [1 2; 3 4]*[5 6;7 8]=[19 22;43 50]
      也就是说两个同维数的矩阵既可以点乘也可以矩阵相乘，只是结果不一样而已！
      *表示线性代数中矩阵相乘的概念！
      
      注意，
      在进行数与数之间的运算时“.*”和“*”是没有区别的，都是表示普通的乘法运算。例：m = 2，n = 4，m.*n = 8， m*n = 8。
      在进行矩阵之间的运算时“.*”和“*”的意义就有所不同了。假设a，b表示两个矩阵，a*b表示矩阵a与矩阵b进行矩阵相乘，a.*b表示矩阵a中的元素与矩阵b中的元素按位置依次相乘，得到的结果将作为新矩阵中相同位置的元素。

函数

diag

• 1. diag函数：sum(diag(a)+diag(a'))可以求矩阵a对角线上的元素之和，不过中间的一个元素会提取2次，diag(a')可以提取副对角线的元素(先将矩阵转置）

  • 当Random是向量时，才构成对角矩阵，当Random是m×n矩阵时，得到的是个向量。比如diag([1 3;2 4])得到向量，diag([1 3])得到2×2矩阵。
  • 可以用来访问对角元素

• 当 v 是向量时，diag(v)得到以 v 的元素为主对角线上元素的对角矩阵；

• 当 v 是矩阵时，diag(v)得到一个列向量，其元素为矩阵 v 主对角线上的元素， diag(v,1)得到矩阵 v 对角线上移一行的元素组成的列向量，diag(v,-1)得到矩阵 v 对 角线下移一行的元素组成的列向量。
  • diag(a)只是diag(a,0)的简写,diag提取出来的都是列矩阵
• 详情查看help

max

• MAX 函数的几种形式

  • (1)max(a)
  • (2)max(a,b)
  • (3)max(a,[],dim)
  • (4)[C,I]=max(a)
  • (5)[C,I]=max(a,[],dim)

• (1)max(a)
  如果 a 是一个矩阵，比如 a=[1,2,3;4,5,6] ，max(a)的意思就是找出矩阵每列的最大值， 本例中：max(a)=[4,5,6]

  • max(a)默认的是max(a,[ ],1)。
  • 矩阵a是行矩阵时，max(a)不再是max(a,[ ],1),而转换为了max(a,[ ],2)。

• (2)max(a,b)
  如果 a 和 b 都是大于 1 维的矩阵，那么要求 a 和 b 的行列的维数都要相等，函数的结 果是比较 a 和 b 中每个元素的大小，比如：
  a=[1,2,3;4,5,6] b=[4,5,6;7,8,3]
max(a,b)=[4,5,6;7,8,6]
  另外，如果 a 和 b 中至少有一个是常数，也是可以的。比如：
  a=[1,2,3;4,5,6] b=3 c=5 max(a,b)=[3,3,3;4,5,6] 相信大家看了例子都明白了函数的意思了吧max(b,c)=5

  • 若a是矩阵，b是数字，那么max(a,b)后，自动把b转换成与a同纬度的矩阵，该矩阵中所有元素都是b，再进行max运算。
• (3)max(a,[],dim)
  这个函数的意思是针对于 2 维矩阵的，dim 是英文字母 dimension 的缩写，意思是维数。
  当 dim=1 时，比较的 a 矩阵的列，也就是和 max（a）的效果是一样的；当 dim=2 时，比较的 是 a 矩阵的行。下面举个例子：
  a=[1,2,3;4,5,6] max(a)=max(a,[],1)=[4,5,6] 比较的第一行和第二行的值
  max(a,[],2)=[3,6]
• (4)[C,I]=max(a)
  C表示的是矩阵 a 每列的最大值， I 表示的是每个最大值对应的下标：
  下面举例说明：
  还是刚才那个例子：a=[1,2,3;4,5,6] [C,I]=max(a)
  结果显示的是 C=[4,5,6] I=[2,2,2] 返回的是最大值对应的行号。
  • C是a每列的最大值矩阵，跟用法一出现的新矩阵一致。I是a每列最大值出现位置对应的行数。
  • 当然，C和I是只是新矩阵的名字，是可以换的。
  • 如果这里有多个相同最大值时，返回的将是第一个最大值的索引。

• (5)[C,I]=max(a,[],dim)
  同理：如果 dim=1 时，其结果和[c,i]=max(a) 是一样的。
  当 dim=2 时，同样上面的矩阵 a，我们运行一下：
  [c,i]=max(a,[],2) 结果是：c=[3,6] i=[3,3] i 返回的是矩阵 a 的列号。

• 文档

• M = max(A) 返回数组的最大元素。
  • 如果 A 是向量，则 max(A) 返回 A 的最大值。
  • 如果 A 为矩阵，则 max(A) 是包含每一列的最大值的行向量。
  • 如果 A 是多维数组，则 max(A) 沿大小不等于 1 的第一个数组维度计算，并将这些元素视为向量。此维度的大小将变为 1，而所有其他维度的大小保持不变。如果 A 是第一个维度长度为零的空数组，则 max(A) 返回与 A 大小相同的空数组。
• M = max(A,[],'all') 查找 A 的所有元素的最大值。(版本不一样，好像无法用)
  • max(max(a))可以用取最大值
  • max(A,[],[1 2]) 计算 A 中所有元素的最大值(版本不一样)

matlab中的sort函数

• 调用格式：
  • B = sort(A)
    • 如果 A 是向量，则 sort(A) 对向量元素进行排序。
    • 如果 A 是矩阵，则 sort(A) 会将 A 的列视为向量并对每列进行排序。
    • 如果 A 是多维数组，则 sort(A) 会沿大小不等于 1 的第一个数组维度计算，并将这些元素视为向量。
  • B = sort(A,dim)返回 A 沿维度 dim 的排序元素。例如，如果 A 是一个矩阵，则 sort(A,2) 对每行中的元素进行排序。
  • B = sort(___,direction)使用上述任何语法返回按 direction 指定的顺序显示的 A 的有序元素。’ascend’ 表示升序（默认值），’descend’ 表示降序。
    • 排序方向必须为 ‘ascend’ 或 ‘descend’
  • B = sort(___,Name,Value)指定用于排序的其他参数。例如，sort(A,'ComparisonMethod','abs') 按模对 A 的元素进行排序。
  • [B,I] = sort(___)还会为上述任意语法返回一个索引向量的集合。I 的大小与 A 的大小相同，它描述了 A 的元素沿已排序的维度在 B 中的排列情况。例如，如果 A 是一个向量，则 B = A(I)。

    - I是B对应的在未排序的矩阵(向量)中的下标
    

• sort(c)从小到大
• sort(c, 'descend')逆序排列(从大到小).

• 例题:

  A = [3 6 5; 7 -2 4; 1 0 -9]
  B = sort(A,2)
  A = 3×3
  
      3     6     5
      7    -2     4
      1     0    -9
  B = 3×3
  
      3     5     6
     -2     4     7
     -9     0     1

• dim - 沿其运算的维度

  • 正整数标量
  • 沿其运算的维度，指定为正整数标量。如果未指定值，则默认值是大小不等于 1 的第一个数组维度。
  • 假定有矩阵 A。sort(A,1) 对 A 的列元素进行排序。
  • sort(A,2) 对 A 的行元素进行排序。

• 注意如果a = 123,此时sort(a)没有作用，因为a是一个数，一个变量，不是集合！！排不了。就像对15这个数一样，sort是对2个及其以上元素排序

• sort(a,1)把矩阵的每一列分别从小到大排成新的矩阵。

• sort(a,2)把矩阵的每一行分别从小到大排成新的矩阵。
• sort(a)默认的是sort(a,1)。
• 矩阵a是行矩阵时，sort(a)不再是sort(a,1),而转换为了sort(a,2)。

MATLAB判断一个数是否整数

if x==fix(x)
% x为整数
%fix（x)为取整
 end

mod函数

• b = mod(a,m)返回a除以m后的余数，其中a是被除数，m是除数。这个函数通常称为模运算，使用b = a - m.*floor(a /m)计算。mod函数遵循mod(a,0)返回a

  %栗子1
  clc,clear;
  a = [-4 -1 7 9];
  m = 3;
  b = mod(a,m)
  a
  %answer
  b =
       2     2     1     0
  a =
      -4    -1     7     9
  
  %栗子2
  clc,clear;
  a = [1 2 3 4];
  m = 2;
  b = mod(a,m)
  c = ~mod(a,m)  %转换为逻辑矩阵
  b =
       1     0     1     0
  c =
       0     1     0     1

常用函数

• 取整
  • fix:向零取整
  • ceil:向上取整
  • floor:向下取整
  • round:四舍五入
• 取余
  • rem:带符号
  • mod:不带符号
• num2str,str2num,size,length
• max等函数的参数是矩阵时，是作用在矩阵各列上
• 

find函数

• 注意matlab中find函数返回的是位置索引（向量，长度大于等于2说明重复出现）
• find()函数的基本功能是返回向量或者矩阵中不为0的元素x的位置索引。(从1开始)a = find(X)
  • 返回前N个非零元素的位置find(A,X)与ind = find(X, k, 'first')
  • 返回最后x个非零值的位置find(A,x,,'last')
  • 如果矩阵中没有该元素，返回值为一个空向量。
• 需要找到其中满足一定条件的元素a = find(x == 4) ，可以用一个表达式或多个表达式
• 文档
• 调用格式:
  • k = find(X)返回一个包含数组 X 中每个非零元素的线性索引的向量。
    • 如果 X 为向量，则 find 返回方向与 X 相同的向量。
    • 如果 X 为多维数组（矩阵），则 find 返回由结果的线性索引组成的列向量。
    • 如果 X 包含非零元素或为空，则 find 返回一个空数组。
  • k = find(X,n)返回与 X 中的非零元素对应的前 n 个索引。
  • k = find(X,n,direction)（其中 direction 为 ‘last’）查找与 X 中的非零元素对应的最后 n 个索引。direction 的默认值为 ‘first’，即查找与非零元素对应的前 n 个索引。
  • [row,col] = find(___)使用前面语法中的任何输入参数返回数组 X 中每个非零元素的行和列下标。
  • [row,col,v] = find(___)还返回包含 X 的非零元素的向量 v。（也就是返回你想找的值，如果不加表达式，条件默认是非零）
• row - 行下标，以向量的形式返回
• col - 列下标，以向量的形式返回，如果 X 是多维数组且 N > 2，则 col 是 X 的 N-1 尾部维度的线性索引。这会保留关系 X(row(i),col(i)) == v(i)。
• find函数以列优先查找
• 假设要查找一个向量中小于 0 的所有元素但没有找到。find 函数将返回一个空的索引向量，表示未找到任何小于 0 的元素。

注意点以及搭配其它函数使用的小技巧

• 要直接查找 X 中满足条件 X < 5 的元素，请使用 X(X < 5)。尽量避免使用 X(find( X < 5) ) 之类的函数调用，因为这种调用中对逻辑矩阵使用的 find 完全没有必要。

• 将 find 与 X>1 之类的关系运算结合在一起执行时，必须记住关系运算的结果是由 1 和 0 组成的逻辑矩阵。例如，命令 [row,col,v] = find(X>1) 会返回由 v 的逻辑值 1 (true) 组成的列向量。

• 假设矩阵为x，则最大值为max(max(x))。 所在位置为：[rows,cols]=find(x==max(max(x)))。蛮有用的

  clc,clear;
  x = [1 2
      3 4
      5 6];
  find(x < 5)
  [rows,cols]=find(x==max(max(x)))
  
  %answer
  ans =
       1
       2
       4
       5
  rows =
       3
  cols =
       2

• len = length(find(X == k));是为了求得矩阵X中值为k的元素个数，等价于下面两种方法：

  • len = length(X(X==k));
  • B = X==k; len=sum(sum(B));

    clc,clear;
    b = [1 2 
        3 4
        5 6
        6 6];
    [r,c] = max(b)
    len1 = length(find(b == 6))
    len2 = length(b(b==6))
    a = b==6; len3=sum(sum(a))
    
    %answer
    r =
         6     6
    c =
         4     3
    len1 =
         3
    len2 =
         3
    len3 =
         3

• [row,col,v] = find(X, ...)

  • 返回X中非零元素的一个列或行向量v，同时返回行和列的索引值。
  • 如果X是一个逻辑表示，则v是一个逻辑矩阵。
  • 输出向量v包含通过评估X表示得到的逻辑矩阵的非零元素。
    • 记住，当你用find指令处理一个逻辑表达的时候，输出向量v不包含输入矩阵的非零元素的索引值。而是包含评估逻辑表达之后返回的非零值。

      clc,clear;
      A= magic(4)
      [r,c,v]= find(A>10);
      r 
      c
      v
      %answer
      A =
          16     2     3    13
           5    11    10     8
           9     7     6    12
           4    14    15     1
      r =
           1
           2
           4
           4
           1
           3
      c =
           1
           2
           2
           3
           4
           4
      v =
           1
           1
           1
           1
           1
           1

栗子(有几种用法，注意一下)

X = [1 0 2; 0 1 1; 0 0 4]
%X = 3×3
     1     0     2
     0     1     1
     0     0     4
k = find(X)
%k = 5×1
     1
     5
     7
     8
     9

%对 X 使用逻辑 not 运算符以查找零值。
k2 = find(~X)  %注意
k2 = 4×1

     2
     3
     4
     6


%在 4×4 幻方矩阵中查找前五个小于 10 的元素
X = magic(4)
%X = 4×4

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

k = find(X<10,5)  %注意可以用表达式！
%k = 5×1

     2
     3
     4
     5
     7

%查看 X 的对应元素。
X(k)
%ans = 5×1

     5
     9
     4
     2
     7


%要查找特定的整数值，请使用 == 运算符。例如，在 1×10 的奇整数向量中查找等于 13 的元素。
x = 1:2:20
%x = 1×10

     1     3     5     7     9    11    13    15    17    19

k = find(x==13)
%k = 7



%要查找非整数值，请基于您的数据使用容差值。否则，由于浮点舍入误差有时会生成空矩阵。
y = 0:0.1:1
%y = 1×11
 0    0.1000    0.2000    0.3000    0.4000    0.5000    0.6000    0.7000    0.8000    0.9000    1.0000
k = find(y==0.3)
%k = 1x0 empty double row vector
%因为浮点数储存精度问题，跟c/c++类似
k = find(abs(y-0.3) < 0.001)  %算法笔记也有类似
%k = 4


%在 4×4 矩阵中查找前 3 个大于 0 且小于 10 的元素。指定两个输出以便将行和列下标返回到这些元素。

X = [18 3 1 11; 8 10 11 3; 9 14 6 1; 4 3 15 21]
%X = 4×4

    18     3     1    11
     8    10    11     3
     9    14     6     1
     4     3    15    21

[row,col] = find(X>0 & X<10,3) %注意注意
%row = 3×1

     2
     3
     4

%col = 3×1

     1
     1
     1

%第一个实例是 X(2,1)，即 8。


%在 3×3 矩阵中查找非零元素。指定三个输出以返回行下标、列下标和元素值。
X = [3 2 0; -5 0 7; 0 0 1]
%X = 3×3

     3     2     0
    -5     0     7
     0     0     1

[row,col,v] = find(X)
%row = 5×1

     1
     2
     1
     2
     3

%col = 5×1

     1
     1
     2
     3
     3

%v = 5×1

     3
    -5
     2
     7
     1