dfs模板
- DFS的重要点在于状态回溯
判出口(终点、越界)-> 剪枝->扩展->标记->递归->还原1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23void dfs()//参数用来表示状态
{
if(到达终点状态){
...//根据题意添加
return;
}
if(越界或者是不合法状态)
return;
if(特殊状态)//剪枝
return ;
for(扩展方式){
if(扩展方式所达到状态合法){
修改操作;//根据题意来添加
标记; //标记可以再开一个另外的数组进行标记
dfs();
(还原标记);
//是否还原标记根据题意
//如果加上(还原标记)就是 回溯法
}
}
}
小技巧
如何获得下一个方向的坐标(此处定义一个方向数组)。
1
2
3
4
5
6
7
8
9
10
11
12int next[4][2]={
{0, 1}//向右走
{1, 0}//向下走
{0, -1}//向左走
{-1, 0}//向上走
};
next[i][0]; //x方向
next[i][1]; //y方向
int dir[4][2]= {0,1,1,0,0,-1,-1,0};
dir[i][0]; //x方向
dir[i][1]; //y方向通过这个方向数组,使用循环就可以方便地得到下一步的坐标。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23int map[6][6];//地图;
bool temp[6][6];//走过的标记;
int dx[4]={0,0,1,-1};//打表;
int dy[4]={-1,1,0,0};//打表;
void walk(int x,int y){//定义walk
if(x==fx&&y==fy)//fx表示结束x坐标,fy表示结束y坐标;
{
total++;//总数增加;
return;//返回,继续搜索;
}
else{
for(int i=0;i<=3;i++)//0——3是左,右,下,上四个方向;
{
if(temp[x+dx[i]][y+dy[i]]==0&&map[x+dx[i]][y+dy[i]]==1)//判断没有走过和没有障碍;
{
temp[x][y]=1;//走过的地方打上标记;
walk(x+dx[i],y+dy[i]);//同i!!!!
temp[x][y]=0;//还原状态;
}
}
}
}就在地图map数组上打标记(自己走过的路)比较简单,走过的路和障碍可能引起混淆
用方向-1.0.1等表示方向的数字作为for循环解决搜索方向问题可能更好
题目
- 典型题一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
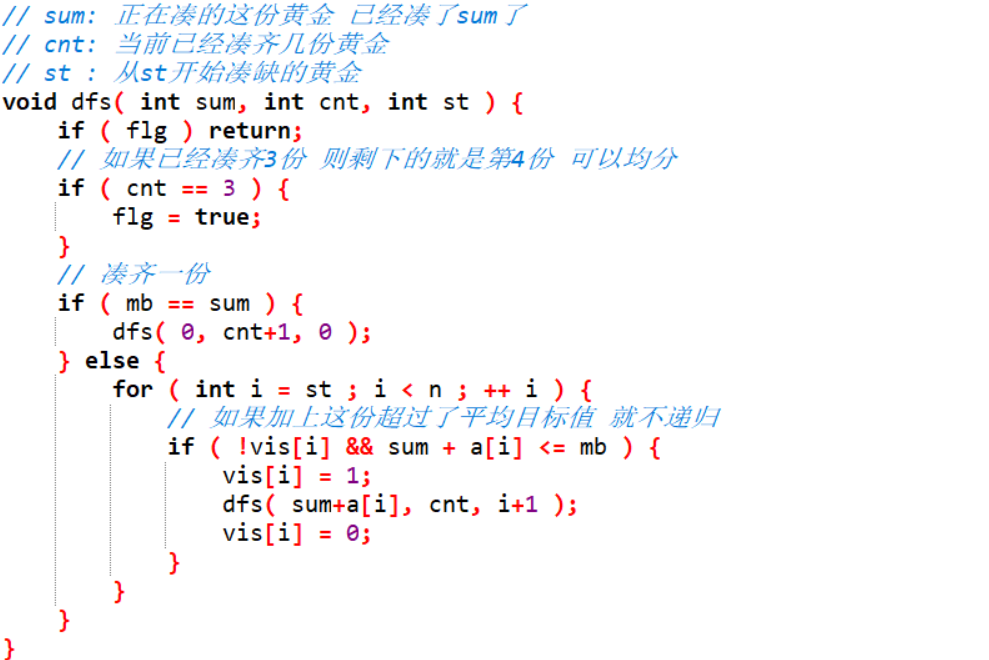
1718年秋第13周任务-地主分财产
时间限制:2秒 内存限制:128兆
55 次提交 1 次通过
题目描述
一位老财主在临终之前想把自己的财产-一箱金条分给四个儿子,为了不引起兄弟之间的矛盾,他想把这箱金条平均分给四个儿子,但是麻烦的是,这箱金条有长有短(但是粗细一样且质地均匀),现在他想知道这箱金条能不能均分成四份(不能将金条裁断),这对于他来说太难了。那么,你能解决这个问题吗?
输入
第一行输入一个整数m<1000, 表示测试用例个数,以下的行是m个测试用例.
每个测试用例的第一个数是金条根数n(4 <= n <= 20),表示金条的根数,接下来的n个整数p1,p2,...,pn,pi为每一根金条的长度,0 <= pi <= 10000。
输出
输出m行,每一行对应每个测试用例,如果这些金条能够均分,则输出"YES",否则输出"NO".
样例输入
2
6 2 3 5 5 1 4
5 12 30 40 20 50
样例输出
YES
NO

- 典型题二:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
2818年秋第13周任务-交友大作战
时间限制:1秒 内存限制:128兆
14 次提交 7 次通过
题目描述
Crw出生在魔仙堡,里面住着很多善良美丽的小魔仙,同时也住着一些想破坏魔仙堡的黑魔仙,Crw很想和善良的小魔仙们交朋友,有一天他决定从家出发出门去看看,于是他偷偷从家里找到一份魔仙堡的地图。地图上标注了一些魔仙的禁地和一些城堡。而且会标注出哪些住的是善良的小魔仙,哪些住的是邪恶的黑魔仙。现在我们Crw每天会到一个城堡中做客并和住在城堡里的所有小魔仙成为朋友,并且下一天能够到相邻的城堡中做客,但是他不能走到黑魔仙的城堡。同时不能走进魔仙堡的禁地。我们知道Crw想和尽可能多的小魔仙成为朋友,那么你能帮他求出他最多能和多少个小魔仙成为朋友吗?
输入
输入数据有多行,每行输入两个整数n和m,分别代表魔仙堡的地图的长和宽。接下来输入的是一个m x n的矩阵代表魔仙堡的地图。其中‘@’代表Crw的家,数字‘1-9’代表该处城堡里住着对应数字的小魔仙,‘#’代表城堡里住着的是黑魔仙,‘*’代表该处是魔仙堡的禁地。最后用0 0结束输入。
输出
结果输出一个数字,代表Crw最多能交到朋友的数量。
样例输入
5 3
@12*3
456**
7#8#9
11 9
1#111111111
1#1#######1
1#1#11111#1
1#1#1###1#1
1#1#11@#1#1
1#1#####1#1
1#1111111#1
1#########1
11111111111
0 0
样例输出
33
58


- 典序例题三:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17第14周任务-dfs&bfs训练(一)
时间限制:1秒 内存限制:128兆
54 次提交 8 次通过
题目描述
没时间编故事了,直接做题吧!问题很简单,现在有两个数n和m,我们有三种操作-1,+1,*2。问:最少需要操作多少次能把n变成m。(0<=n,m<=1000000)
输入
输入数据有多组,每行输入两个整数n和m
输出
每行输出一个数字代表最少操作次数
样例输入
5 17
样例输出
4
题目分析:
本题分析和思路参照我上周在群里发的周任务提示。通常我们在广搜中需要用到的队列,我们都用c++stl中现有的队列,并且需要引入头文件#include<queue>
定义方式如下:
queue<datetype> queue_name;

- 四
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20第14周任务-dfs&bfs训练(二)
时间限制:3秒 内存限制:128兆
21 次提交 7 次通过
题目描述
我们来做一个经典问题:n皇后问题
N皇后问题是指在一个N*N的棋盘上,放置N个皇后:
1、每行至多一个
2、每列至多一个
3、对角线方位上,不能有其他皇后
问题是最多有多少种放置方案。
输入
每行输入一个正整数n,代表需要放置的皇后个数。
输出
每行输出一个整数,代表最大放置方案数
样例输入
8
样例输出
92
题目分析:
本题分析参照周任务提示,需要注意这里标记数组的用法,节约了遍历检查的时间开销。

- 地图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
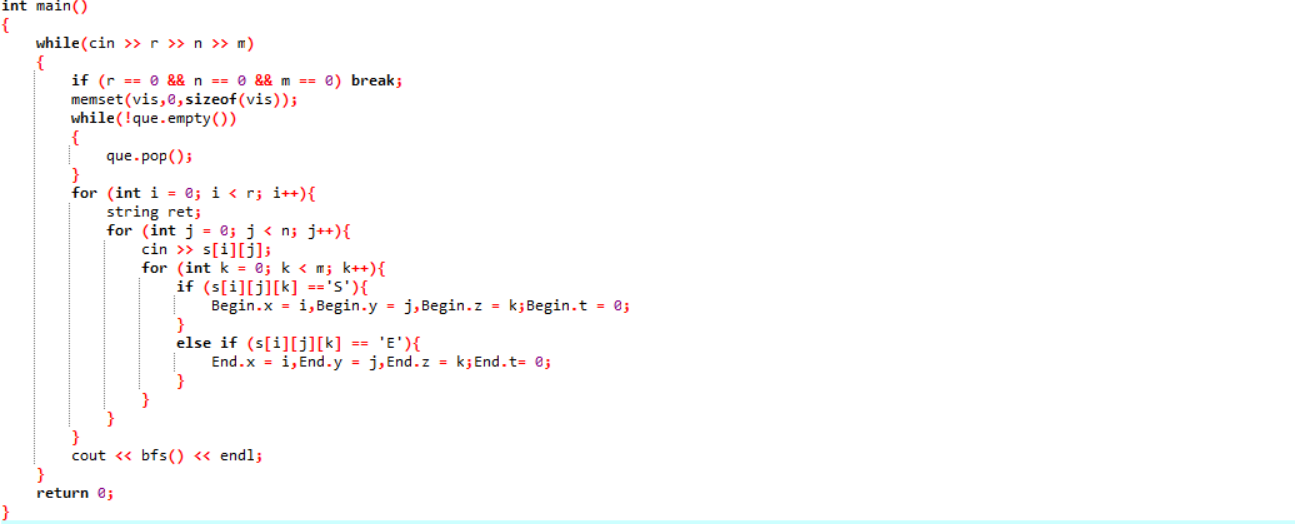
36第14周任务-dfs&bfs训练(三)
时间限制:1秒 内存限制:128兆
30 次提交 4 次通过
Crw家住在魔仙堡我们都已经知道了,他喜欢和小魔仙交朋友我们也知道了。那么现在他膨胀了,他觉得魔仙堡的小姐姐已经满足不了他了,所以他决定出去看看。我们之前知道的魔仙堡有一张地图,标明了魔仙堡的地理情况,但实际上魔仙堡存在很多维度,每一个维度都是平行而且大小相同的,我们不光能在一同平面内移动,还能在上下空间中传送,不同维度的空间坐标是完全一一对应的,因此只能传送到相邻维度空间中相同的坐标处。现在我们知道魔仙堡的出口就在某一维的空间之中,但是Crw很迫切,每一秒他能向前后左右上下六个方向移动一个坐标,他想知道他最快多少秒就能走出魔仙堡。那么请你来帮他解决这个问题吧。
输入
有多组数据,每组数据第一行有三个正整数k,n,m。k代表魔仙堡的维度,n和m代表魔仙堡每个维度是一个n x m大小的平面。接下来输入k个n x m的矩阵,每个矩阵用一个空行隔开,代表每个平面的地图。其中‘S’代表Crw的家,‘E’代表魔仙堡的出口,‘.’代表可以移动的空地,‘#’代表不能移动到的危险位置。最后用三个0代表停止输入。
输出
每组数据输出一个数字,代表Crw最快逃离魔仙堡的时间。如果无法找到出口则输出-1。
样例输入
3 4 5
S....
.###.
.##..
###.#
#####
#####
##.##
##...
#####
#####
#.###
####E
1 3 3
S##
#E#
###
0 0 0
样例输出
11
-1
题目分析:
简单三维地图的搜索


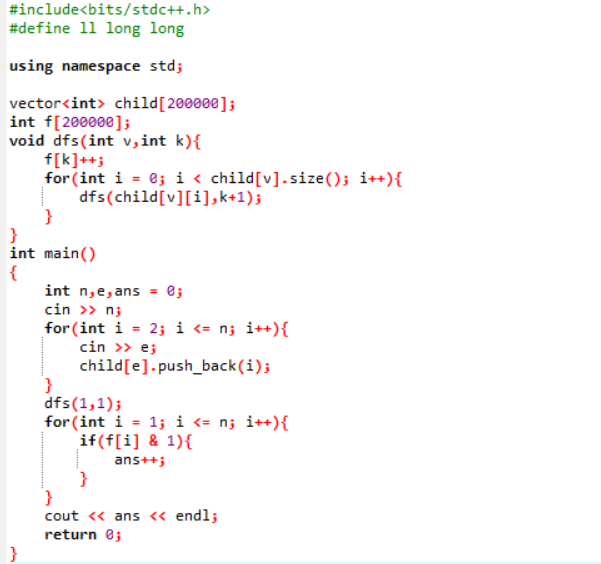
- 人参果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23第14周任务-dfs&bfs训练(四)
时间限制:1秒 内存限制:128兆
7 次提交 1 次通过
题目描述
传说在三大有一颗神奇的人参果树,一年结一次果,它总共n个节点,第一个节点是他的树根,其他节点都在树的上端。除了根节点,每个节点i(i>1)下面都连接有一个pi( pi < i )节点,这颗树很神奇,每年到了结果的时候,每个节点会同时结下一个人参果。然后成熟了开始掉落,但他不会像牛顿的苹果树那样自由掉落,而是每一秒钟下滚到它的连接着的下一个靠近树根的节点。直到滚到树根为止。但是我们知道牛x的东西都是脾气很大的,如果我们在同一节点同时滚落了多个人参果,那么他们会两两消亡。所以我们的问题是最后我们在根节点处能收到多少个人参果。
输入
第一行输入一个正整数n,代表树总共的节点个数(1<=n<=100000)。
第二行输入n-1个数pi(2<=i<=n),分别代表第i个节点连接的是第pi个节点,即人参果滚落的下一个节点。
输出
输出一个数字代表最后在根节点能够收到的人参果个数。
样例输入
5
1 2 2 2
样例输出
3
提示
比如样例中有5个节点,根节点是1号,下面四个数字分别代表2号节点连接的是1号,3,4,5号节点连接的都是2号。最后能过收获1号节点的一个人参果,然后下一秒2号节点的人参果掉落到1号再次收获一个,同时,3,4,5号节点的人参果同时滚落到2号会抵消掉2个,剩下一个最后滚落到1号节点被收获,所以结果是3个
问题分析:
本题和本周周任务中涉及到的二叉树有些联系,本题也可以模拟成一个树,但不是一颗二叉树,而是一个普通的树,每个节点连接着零个或多个子节点,每个节点上结一个果实。同时向下滚落。如果我们用树的遍历的方式去暴力模拟每一种情况,看最后剩余的果实个数肯定会超时。所以我们需要找规律,很明显我们发现无论有多少个节点,每一层最多剩下一个或零个果实。我们把根节点当做第一层,也就是深度为1,与根节点直接相连的节点为第二层,依次类推,每一层节点的个数为偶数时,则所有的果实都相互抵消,节点个数为奇数则剩余一个。因此我们用dfs搜索每一层(深度相同)的节点个数,并统计下来。最后求出每层剩余果实之和即为最后根节点剩余果实数目。
注意:
这里我用到vector,同样是c++stl当中的一种数据结构,我们通常在算法当中常用到vector来表示树和图这些数据结构。这里也可以用结构体替代,后面会向大家介绍c++stl中一些常用的数据结构的用法。