数学原理
- 一个数 n 如果是合数,那么它的所有的因子不超过sqrt(n)–n的开方
- 质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数
- 质数大于等于2 不能被它本身和1以外的数整除
素数筛选法
- 素数是数学中一个很重要的数,很多算法中都需要用到素数相关的性质,因此传统的暴力循环求素数的效率显得十分低效,这里我们有两种高效求1~n以内的素数的方法。需要大家掌握,特别是欧拉筛法里面用到一点数学性质,大家可自行百度欧拉筛法掌握具体的原理,以后的出现的算法中还会出现。
欧拉筛法-时间复杂度(n)
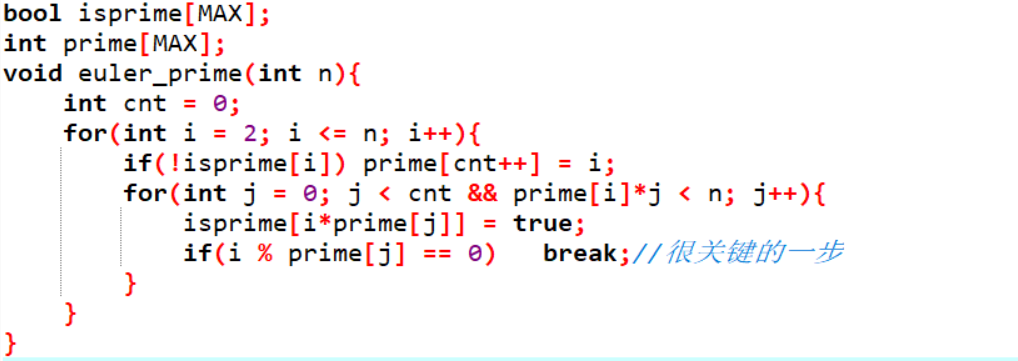
- 回顾经典的Eratosthenes筛法,它可能对同一个质数筛去多次。那么如果用某种方法使得每个合数只被筛去一次就变成是线性的了。不妨规定每个合数只用其最小的一个质因数去筛,这便是欧拉筛了。
- 最简单的素数筛法是这样的:10000000内的素数,用这个筛选法可以大大的降低时间复杂度
1.开一个大的bool型数组prime[],大小就是n+1就可以了.先把所有的下标为奇数的标为true,下标为偶数的标为false.
2.然后:1
2
3
4
5
6
7
for( i=3; i<=sqrt(n); i+=2 )
{
if(prime)
for( j=i+i; j<=n; j+=i ) prime[j]=false;
}
3.最后输出bool数组中的值为true的单元的下标,就是所求的n以内的素数了。
原理很简单,就是当i是质(素)数的时候,i的所有的倍数必然是合数。如果i已经被判断不是质数了,那么再找到i后面的质数来把这个质数的倍数筛掉。
原理
- No.1使用 合数=最大因数(除1和本身外)最小质因数 的原理来筛,每个数只会被筛一次
对于每个数i,令它是某数的最大因数,然后从小到大地找<=i的素数j,则ij是合数
直到找到某个j使得i%j == 0,因为再往后的话,j’> i的某个因子,我们能交换j’和i的这个因子,所以i不是ij’的最大因数(或者说ij’的最小质因数是刚才的那个j),再往后做没有意义
No.2回顾经典的Eratosthenes筛法,它可能对同一个质数筛去多次。那么如果用某种方法使得每个合数只被筛去一次就变成是线性的了。
不妨规定每个合数只用其最小的一个质因数去筛,这便是欧拉筛了。No.3
线性筛有两个地方与一般筛不同:
1.两层循环的顺序不同(一般筛是第一维prime[i] 第二维j,欧拉筛是第一维i 第二位prime[j])
2.一行神奇的代码:
if(i%prime[j]==0)break;
prime[]数组中的素数是递增的,当i能整除prime[j],那么iprime[j+1]这个合数肯定被prime[j]乘以某个数筛掉。
因为i中含有prime[j],prime[j]比prime[j+1]小,即 `i=kprime[j],那么iprime[j+1]=(kprime[j])prime [j+1]=k’prime[j],接下去的素数同理。所以不用筛下去了。因此,在满足i%prime[j]==0`这个条件之前以及第一次
满足改条件时,prime[j]必定是prime[j]*i的最小因子。
No.4 证明分两部分。首先证每个合数都会被筛到(正确性),其次证每个合数只会被筛到一次(复杂度)。
每个合数都会被筛到
设有一合数 (为质数)
则一定会在 时被筛去(此时 ),因为对于小于 的质数,一定不会被 整除
每个合数都只会被筛到一次
与上面一样,还是设有一合数 ( 为质数)
倘若存在一个质因子 也筛去了,那么此时 。
o,此时在内层循环中已经早早地break掉了,因为 。
o,此时还没加进质数表QwQ(顺便一提:这种情况只有可能在 时发生)
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
void euler_sieve(int n) {
totPrimes = 0;
memset(flag, 0, sizeof(flag));
for (int i = 2; i <= n; i++) {
if (!flag[i])
primes[totPrimes++] = i;
for (int j = 0; i * primes[j] <= n; j++) {
flag[i*primes[j]] = true;
if (i % primes[j] == 0) break;
}
}
}
j < totPrimes为何不加?
o当 为质数时,内层循环会在最后一个质数(也就是 自己)终止。
o当 为合数时,内层循环会在它的第一个质因数终止。
当然加了也没有问题
埃拉特斯特尼筛法,时间复杂度(nlogn)
